I was wondering how you can know that your formula is correct
when you are discovering it. In this post I am sharing some of my findings related to it.
The triangle can be thought of as half of rectangle, so its
area should also be half,
½ ar(rectangle) = ½ (ab)
But in this sense, to discover this formula you need to know
the area of a rectangle.
Heron’s formula gives the area of triangle without using it,
√s(s-a)(s-b)(s-c)
Where s = ½ (a+b+c)
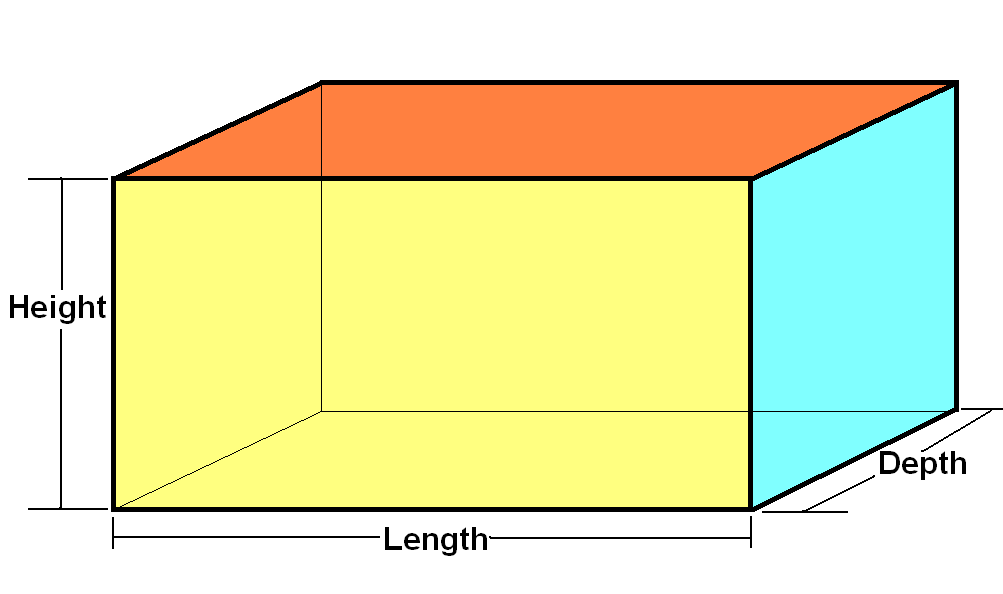
Now let’s take another formula, the area of a cuboid which
is,
2(lb+bh+hl)
This formula also involves the area of rectangle. There are three
pairs of identical rectangles, so their area lb, bh, hl adds up twice to give
the formula 2(lb+bh+hl).
Similarly in a cube all the sides have equal length so the
area of cube is,
2(3a²) = 6a²
I tried to discover formula of triangle without using any
other formula but I failed to do so. So how our ancient mathematicians discovered them and how they knew that
their formulas are correct? I will try to find answers of these questions in future.
But the formulas
discovered in ancient times were not always correct. Like an Egyptian formula
for finding the area of a circle was to take the square of 8/9 of the circle’s
diameter. It’s not correct because if we compare it with the formula we now know, then we get very less accurate value of pi.
Pi r² =
(8/9)²(2r)²
Pi = 256/81 = 3.1604…